Chapitre 6 Les opérations spatiales sur les données

Les opérations spatiales sont des opérations prenant nos données en entrée pour en sortir un résultat dépendant de leur composante spatiale (forme, localisation).

Dans ce chapitre, nous allons utiliser les packages suivants.

# CRAN
library(mapview)
library(sf)
library(tidyverse)

Nous utiliserons les données de la table des régions de la France métropolitaine et des établissements publics de coopération intercommunale (EPCI)⁶ de la France Métropolitaine

load("extdata/admin_express.RData")

glimpse(epci_geo)

Rows: 1,241
Columns: 5
$ ID        <fct> EPCI00000000000000000001, EPCI00000000000000000002, EPCI0000…
$ CODE_EPCI <fct> 200000172, 200000438, 200000545, 200000628, 200000800, 20000…
$ NOM_EPCI  <fct> "CC Faucigny-Glières", "CC du Pays de Pontchâteau Saint-Gild…
$ TYPE_EPCI <fct> CC, CC, CC, CC, CC, CC, CC, CC, CC, CC, CA, CC, CC, CC, CC, …
$ geometry  <MULTIPOLYGON [m]> MULTIPOLYGON (((964676 6561..., MULTIPOLYGON ((…

glimpse(departements_geo)

Rows: 96
Columns: 6
$ ID        <fct> DEP000000000000000000001, DEP000000000000000000002, DEP00000…
$ NOM_DEP   <fct> AIN, HAUTE-CORSE, AISNE, CORSE-DU-SUD, ALLIER, ALPES-DE-HAUT…
$ INSEE_DEP <fct> 01, 2B, 02, 2A, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, …
$ INSEE_REG <fct> 84, 94, 32, 94, 84, 93, 93, 93, 84, 44, 76, 44, 76, 76, 93, …
$ AREA      [m^2] 5774813520 [m^2], 4722274798 [m^2], 7419025664 [m^2], 403749…
$ geometry  <MULTIPOLYGON [m]> MULTIPOLYGON (((839096 6563..., MULTIPOLYGON ((…

glimpse(regions_geo)

Rows: 13
Columns: 4
$ ID        <fct> REG000000000000000000001, REG000000000000000000002, REG00000…
$ NOM_REG   <fct> AUVERGNE-RHONE-ALPES, BOURGOGNE-FRANCHE-COMTE, BRETAGNE, CEN…
$ INSEE_REG <fct> 84, 27, 53, 24, 94, 44, 32, 11, 28, 75, 76, 52, 93
$ geometry  <MULTIPOLYGON [m]> MULTIPOLYGON (((974065 6594..., MULTIPOLYGON (((880573 6730.…

6.1 Filtrer

Nous souhaitons par exemple filtrer nos EPCI sur les EPCI du département de Loire-Atlantique.

departement_44 <- departements_geo %>%
  filter(INSEE_DEP == "44")

epci_d44 <- epci_geo[departement_44, , op = st_within]

mapview(list(departement_44, epci_d44), zcol = list("NOM_DEP", "NOM_EPCI"), legend = FALSE)

L’opération de filtre sur les données spatiales fonctionne en prenant la table en entrée (epci_geo), la table avec laquelle on souhaite définir les lignes à garder (departement_44), et l’opérateur qui va définir le test entre les deux géométries. Ici cet opérateur est st_within(x, y), qui renvoie TRUE si la géométrie de x est contenue à l’intérieur de celle de y.

On peut spécifier différents prédicats spatiaux pour réaliser ce filtre.

En deuxième argument des [ , , ], on peut ajouter, comme dans une opération [ classique de R, les colonnes que l’on souhaite garder.

On peut aussi écrire en tidyverse :

# 1er méthode
epci_d44 <- epci_geo %>% 
  st_filter(departement_44, .predicate = st_within)

# 2e méthode
epci_d44 <- epci_geo %>%
  filter(st_within(., departement_44, sparse = FALSE))

Il faut noter la présence du paramètre sparse = FALSE. L’option sparse est abordée dans la partie Prédicats spatiaux. Il faut retenir que pour utiliser les prédicats à l’intérieur de la fonction filter, il faut utiliser l’option sparse = FALSE.

On voit ici que le résultat n’est pas très concluant : il manque 3 EPCI du département, ceux qui sortent des frontières de celui-ci. Prenons un buffer autour du département.

Qu’est ce qu’un buffer ? C’est un tampon qui va nous permettre d’appliquer une transformation sur un objet vectoriel.

A partir d’une couche de départ de type ponctuel, linéaire ou polygonal, le buffer va créer une nouvelle couche vectorielle. La géométrie de cette couche représente des objets surfaciques dont les frontières sont positionnées à une distance euclidienne, définie par l’utilisateur, des limites des objets vectoriels de la couche de départ.

La fonction qui permet de faire cela avec sf s’appelle st_buffer().

st_buffer() prend en paramètre :

un objet de classe sf
une distance dont l’unité est définie par celle de l’objet sf, que l’on peut obtenir comme ceci st_crs(x)$units.

departement_44_buffer <- departement_44 %>%
  st_buffer(dist = 5000)

mapview(list(departement_44_buffer, departement_44), legend = FALSE, 
        layer.name = c("Loire-Atlantique avec un buffer de 5 km", "Loire-Atlantique"), 
        zcol = list("NOM_DEP", "NOM_DEP"), col.regions = list("#440154FF", "#FDE725FF"))

epci_d44_buffer <- epci_geo[departement_44_buffer, , op = st_within]

mapview(list(departement_44_buffer, epci_d44_buffer), zcol = list("NOM_DEP", "NOM_EPCI"), legend = FALSE)

On récupère 2 des 3 EPCI manquant ainsi. Celui qui manque est l’EPCI de Redon qui est à cheval sur la Loire-Atlantique, le Morbihan et l’Île et Vilaine. Une méthode pour le récupérer est de prendre l’opérateur de filtre st_intersect au lieu de st_within en utilisant un buffer légèrement négatif de notre département pour ne pas récupérer tous les EPCI limitrophes.

departement_44_buffer_negatif <- departement_44 %>%
  st_buffer(dist = -2000)

epci_d44 <- epci_geo[departement_44_buffer_negatif, , op = st_intersects]

mapview(list(departement_44, epci_d44), zcol = list("NOM_DEP", "NOM_EPCI"), legend = FALSE)

On aurait pu obtenir le même résultat en prenant les EPCI à l’intérieur du département 44 (avec st_within) ainsi que les EPCI qui chevauchent (avec st_overlaps) le département 44.

epci_d44 <- epci_geo %>%
  filter(st_within(., departement_44, sparse = FALSE) | st_overlaps(., departement_44, sparse = FALSE))

mapview(list(departement_44, epci_d44), zcol = c("NOM_DEP", "NOM_EPCI"), legend = FALSE)

6.2 Prédicats spatiaux

Les prédicats spatiaux décrivent les relations spatiales entre objets. Pour bien les illustrer, on va utiliser quelques données de notre création.

Nous allons utiliser un polygone (a), des lignes (l) et des points (p), que nous créons à partir de leur coordonnées.

# polygone (a - orange)
a_poly <- st_polygon(list(rbind(c(-1, -1), c(1, -1), c(1, 1), c(-1, -1))))
a <- st_sfc(a_poly)

# lignes (l - bleues)
l1 <- st_multilinestring(list(rbind(c(0.5, -1), c(-0.5, 1))))
l2 <- st_multilinestring(list(rbind(c(.9, -.9), c(.5, 0))))
l <- st_sfc(l1, l2)

# multi-points (p - noirs)
p_matrix <- matrix(c(0.5, 1, -1, 0, 0, 1, 0.5, 1), ncol = 2)
p_multi <- st_multipoint(x = p_matrix)
p_multi
p <- st_cast(st_sfc(p_multi), "POINT")

La fonction st_cast sert à passer d’un type de géométrie à l’autre, ici on transforme un multi-points en points.

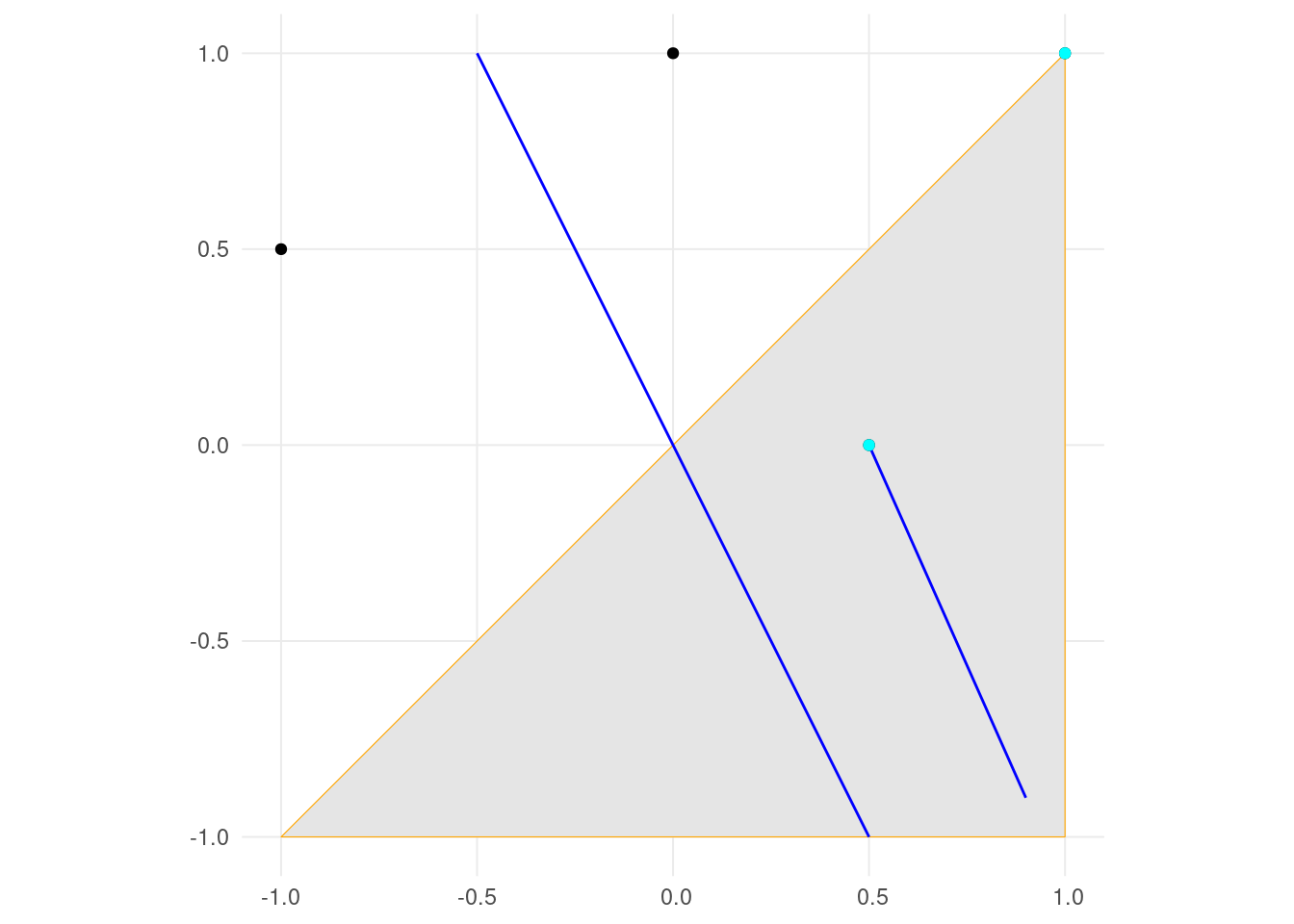
A partir de ces objets, on peut se poser les questions suivantes :

Quels sont les points de p contenus dans le triangle a ?
Quels sont les points de p qui ne sont pas contenus dans le triangle a ?
Quels sont les points de p qui touchent le triangle a ?
Quelles sont les lignes de l contenues dans a ?

Les prédicats spatiaux servent à répondre à ces questions et sf contient une liste de fonctions dédiée à l’une ou l’autre de ces questions.

st_intersects() permet de répondre à la première question, à savoir quels points de p sont dans a.

st_intersects(p, a)

Sparse geometry binary predicate list of length 4, where the predicate
was `intersects'
 1: 1
 2: 1
 3: (empty)
 4: (empty)

L’opposé de st_intersects() est st_disjoint() : st_disjoint(x,y) renvoie TRUE pour les objets de x non reliés à y.

st_disjoint(p, a)

Sparse geometry binary predicate list of length 4, where the predicate
was `disjoint'
 1: (empty)
 2: (empty)
 3: 1
 4: 1

Le résultat de cette opération est une liste. Par défaut, la fonction st_intersect() renvoie une matrice creuse⁷. Cette structure permet d’économiser de la mémoire en n’enregistrant que les relations qui existent. Sur une opération de ce type, le gain est peu évident, mais quand on travaille sur des objets plus complexes, le gain est appréciable.

Si on souhaite mieux utiliser cette information, on peut vouloir privilégier la matrice dense, qui renvoie une matrice de booléen pour chaque relation possible.

Pour cela on peut utiliser l’option sparse = FALSE, ‘sparse’ signifiant en anglais ‘clairsemé’.

st_intersects(p, a, sparse = FALSE)

      [,1]
[1,]  TRUE
[2,]  TRUE
[3,] FALSE
[4,] FALSE

st_within() est une variante de st_intersect() qui ne renvoie TRUE que pour les points strictement à l’intérieur du polygone.

st_within(p, a, sparse = FALSE)

      [,1]
[1,]  TRUE
[2,] FALSE
[3,] FALSE
[4,] FALSE

Une variante de st_within() permet d’ajouter un critère de distance pour intégrer des points presque dans le polygone, st_is_within_distance().

st_is_within_distance(p, a, dist = 0.8)

Sparse geometry binary predicate list of length 4, where the predicate
was `is_within_distance'
 1: 1
 2: 1
 3: (empty)
 4: 1

st_touches() permet de récupérer les points qui touchent le polygone sans sans être à l’intérieur du polygone.

st_touches(p, a, sparse = FALSE)

      [,1]
[1,] FALSE
[2,]  TRUE
[3,] FALSE
[4,] FALSE

st_contains(x,y) est équivalent à st_within(y,x). Par exemple si nous voulons savoir lesquelles de nos lignes l sont contenues dans a.

st_contains(a, l, sparse = FALSE)

      [,1] [,2]
[1,] FALSE TRUE

Equivalent à :

st_within(l, a, sparse = FALSE)

      [,1]
[1,] FALSE
[2,]  TRUE

st_crosses() renvoie TRUE si l’intersection des deux géométries est une géométrie de dimension n-1 ou n est le maximum des dimensions des deux objets et si l’intersection est à l’intérieur des deux objets.

st_crosses(l, a, sparse = FALSE)

      [,1]
[1,]  TRUE
[2,] FALSE

Il existent encore d’autres prédicats qu’on ne détaillera pas ici :

st_covers()
st_covered_by()
st_equals() et st_equals_exact()
st_contains_properly()
st_overlaps()

6.2.1 Exercice 1 - manipuler des objets sf

Créer un objet contenant les points de p qui intersectent le polygone a, à partir du code suivant :

library(sf)
library(tidyverse)
# polygone (a - orange)
a_poly <- st_polygon(list(rbind(c(-1, -1), c(1, -1), c(1, 1), c(-1, -1))))
a <- st_sfc(a_poly)
# lignes (l - bleues)
l1 <- st_multilinestring(list(rbind(c(0.5, -1), c(-0.5, 1))))
l2 <- st_multilinestring(list(rbind(c(.9, -.9), c(.5, 0))))
l <- st_sfc(l1, l2)
# multi-points (p - noirs)
p_matrix <- matrix(c(0.5, 1, -1, 0, 0, 1, 0.5, 1), ncol = 2)
p_multi <- st_multipoint(x = p_matrix)
p <- st_cast(st_sfc(p_multi), "POINT")

Résultat attendu :

# A tibble: 2 × 1
        p
  <POINT>
1 (0.5 0)
2   (1 1)

Visualisation graphique :

6.3 Les jointures spatiales

Les jointures attributaires se basent sur un appariement entre une liste des variables présentes dans les deux tables.

Les jointures spatiales se basent sur un appariement géographique, c’est à dire sur un espace géo commun.

6.3.1 Jointure de points avec des polygones

Ce cas est relativement simple, une jointure spatiale entre une liste de points et une liste de polygones va attribuer pour chaque point le ou les polygones auquel il appartient.

On va utiliser ici le fichier sirene du département de Loire Atlantique géocodé par Christian Quest⁸. Prenons les entreprises de production de sel (code APE ‘0893Z’) sur ce département et regardons dans quelle partie du territoire elles se trouvent.

load("extdata/sirene.RData")

sirene44_sel <- sirene44 %>%
  filter(APET700 == "0893Z")

mapview(list(departement_44, epci_d44, sirene44_sel), zcol = list("NOM_DEP", "NOM_EPCI", "NOMEN_LONG"), legend = FALSE)

Nous allons réaliser une jointure spatiale pour récupérer le code sirene de l’EPCI où se trouve chaque entreprise.

sirene44_sel_avec_code_epci <- sirene44_sel %>%
  st_join(epci_geo)

mapview(list(departement_44, epci_d44, sirene44_sel_avec_code_epci), zcol = list("NOM_DEP", "NOM_EPCI", "NOM_EPCI"), legend = FALSE)

Une jointure entre deux couches de données géographiques demande à ce que celles-ci partagent la même projection.

6.3.2 Jointure de polygones avec des polygones

A la différence des appariements entre points et polygones, la jointure spatiales entre deux couches de polygones nécessite quelques critères complémentaires : souhaite-t-on joindre deux polygones dès qu’ils s’intersectent ? Souhaite-t-on joindre à un polygone de la première couche à celui de la deuxième avec lequel il partage le plus de surface en commun ?

Par exemple, imaginons que nous voulions joindre notre couche des EPCI avec celle des départements, souhaite-t-on que l’EPCI de Redon se retrouve apparié avec tous les départements auxquels il appartient, ou seulement le département dans lequel il est principalement situé ?

epci_d44_avec_departement <- epci_d44 %>%
  st_join(departements_geo %>% st_buffer(dist = -1000))

names(epci_d44_avec_departement)

 [1] "ID.x"      "CODE_EPCI" "NOM_EPCI"  "TYPE_EPCI" "ID.y"      "NOM_DEP"  
 [7] "INSEE_DEP" "INSEE_REG" "AREA"      "geometry"

epci_d44_avec_departement %>%
  select(NOM_EPCI, NOM_DEP) %>%
  group_by(NOM_EPCI) %>%
  tally() %>%
  arrange(-n)

# A tibble: 17 × 3
   NOM_EPCI                                          n                  geometry
   <fct>                                         <int>        <MULTIPOLYGON [m]>
 1 CA Redon Agglomération                            3 (((306620 6741720, 30626…
 2 CA de la Presqu'île de Guérande Atlantique (…     2 (((276339 6716135, 27628…
 3 CC du Pays d'Ancenis                              2 (((371339 6714790, 37131…
 4 CA Clisson Sèvre et Maine Agglo                   1 (((363286 6675340, 36313…
 5 CA de la Région Nazairienne et de l'Estuaire…     1 (((302551 6716906, 30254…
 6 CA Pornic Agglo Pays de Retz                      1 (((308476 6686309, 30859…
 7 CC Châteaubriant-Derval                           1 (((352474 6745979, 35243…
 8 CC d'Erdre et Gesvres                             1 (((344433 6712377, 34443…
 9 CC de Grand Lieu                                  1 (((350722 6678570, 35073…
10 CC de la Région de Blain                          1 (((347300 6718329, 34716…
11 CC de Nozay                                       1 (((348972 6729772, 34899…
12 CC du Pays de Pontchâteau Saint-Gildas-des-B…     1 (((316649 6727168, 31667…
13 CC du Sud-Estuaire                                1 (((312929 6700671, 31338…
14 CC Estuaire et Sillon                             1 (((321943 6705416, 32193…
15 CC Sèvre et Loire                                 1 (((369368 6686432, 36928…
16 CC Sud Retz Atlantique                            1 (((336398 6673676, 33641…
17 Nantes Métropole                                  1 (((353637 6695899, 35362…

Une jointure classique va donc rattacher 3 EPCI à plus de 1 département.

Avec l’option largest = TRUE la jointure va attribuer aux EPCI le département avec lequel il partage le plus de surface. On voit ici que tout les EPCI adhérents à la Loire-Atlantique se retrouvent alors rattachés à la Loire-Atlantique.

epci_d44_avec_departement <- epci_d44 %>%
  st_join(departements_geo %>% st_buffer(dist = -1000), largest = TRUE)

mapview(list(departement_44, epci_d44, sirene44_sel_avec_code_epci), zcol = list("NOM_DEP", "NOM_EPCI", "NOM_EPCI"), 
        legend = FALSE)

st_join() utilise par défaut le prédicat st_intersects, dans le paramètre join.

Après une jointure spatiale, le dataframe résultat contient la géométrie du jeu de données de gauche (càd le 1er jeu de données passé dans les arguments de st_join()).

6.3.3 Exercice 2 : exploitation des données DVF en API

Le but de cet exercice va être d’exploiter les données DVF sur les transactions immobilières dans l’ancien et la carte des quartiers de Nantes pour obtenir des indicateurs des transactions par quartier.
On va utiliser pour DVF l’API mise en place par Christian Quest : http://api.cquest.org/dvf.

## Activation des packages
library(httr)
library(jsonlite)
library(sf)
library(tidyverse)
get_dvf <- GET("http://api.cquest.org/dvf?code_commune=44109")
dvf_content <- content(get_dvf, "text", encoding = "UTF-8")
dvf_json <- fromJSON(dvf_content)$resultats %>%
  # On ne garde que les données avec une géolocalisation valide, un prix et une surface renseignés.
  filter(!is.na(lon), !is.na(lat), !is.na(valeur_fonciere), !is.na(surface_relle_bati))
dvf <- st_as_sf(dvf_json, coords = c("lon", "lat"), crs = 4326)

Contour des quartiers de Nantes, ils proviennent de Nantes Métropole Open Data :https://data.nantesmetropole.fr

quartier_nantes <- st_read("https://data.nantesmetropole.fr/explore/dataset/244400404_quartiers-communes-nantes-metropole/download/?format=geojson&disjunctive.libcom=true&refine.libcom=Nantes&timezone=Europe/Berlin&lang=fr")
quartier_nantes <- st_set_crs(quartier_nantes, 4326)

On veut produire les infos suivantes par quartier et année :

Volume de ventes (nb)
Pourcentage de maisons dans les ventes
Prix moyen au m2 par type de bien

Résultat attendu :

Rows: 66
Columns: 8
$ quartier            <chr> "Ile de Nantes", "Ile de Nantes", "Ile de Nantes",…
$ annee_mutation      <dbl> 2014, 2015, 2016, 2017, 2018, 2019, 2014, 2015, 20…
$ nb_ventes           <dbl> 255, 346, 405, 464, 475, 221, 212, 203, 196, 224, …
$ pourcentage_maison  <dbl> 1.960784, 2.312139, 2.962963, 1.293103, 1.263158, …
$ prix_m2_appartement <dbl> 4227.436, 2720.641, 3583.049, 3496.280, 3574.651, …
$ prix_m2_maison      <dbl> 3208.333, 2961.019, 19695.106, 3519.273, 4144.621,…
$ prix_m2_ensemble    <dbl> 4187.948, 2728.811, 4208.121, 3496.700, 3587.453, …
$ geometry            <POLYGON [°]> POLYGON ((-1.518491 47.2105..., POLYGON ((…

6.4 Les mesures

Contrairement aux opérations précédentes qui sont binaires, les opérations de mesure sont continues.

6.4.1 Calcul de surface

Le calcul de surface se fait à l’aide de la fonction st_area(). Le résultat sera exprimé dans l’unité du crs.

st_area(epci_d44)

Units: [m^2]
 [1] 327171752 451105821 311573694 277485664 425120290 884405865 313277739
 [8] 995291184 533909100 300537854 214300118 509590978 275642240 865087496
[15] 223059032 396227313 333955602

6.4.2 Matrice de distances

Les distances se calculent avec la fonction st_distance().

centres_departements_pdl <- st_centroid(departements_geo) %>%
  filter(INSEE_REG == "52")

st_distance(centres_departements_pdl)

Units: [m]
          1        2         3         4         5
1      0.00 84564.06 115956.62 159032.47  81705.88
2  84564.06     0.00  84434.09  89195.57  97175.56
3 115956.62 84434.09      0.00  67722.46 170458.60
4 159032.47 89195.57  67722.46      0.00 186168.94
5  81705.88 97175.56 170458.60 186168.94      0.00

Trois choses à noter sur le résultat :

st_distance() retourne une matrice…
… contenant toute les distances calculables 2 à 2…
…et qui a un paramètre Units nous donnant l’unité de mesure des distances calculées.

Ici on calcule notre matrice sur un seul objet. Vous pouvez calculer des distances entre deux objets x et y de classe sf. Dans ce cas il fera le calcul des distances pour toutes les combinaisons possibles d’objets de x et de y. Une option de st_distance() vous permet de limiter le résultat aux calculs 2 à 2 : by_element = TRUE. Dans ce cas le résultat est un vecteur.

6.4.3 Identification du plus proche voisin

Un besoin fréquent en géomatique est d’identifier l’objet le plus proche d’un autre. La fonction qui permet cela est st_nearest_feature().

Prenons l’ensemble des départements français, et trouvons celui de la région qui leur est le plus proche. On va utiliser les centroïdes pour alléger le calcul.

index_dep_pdl <- st_nearest_feature(
  departements_geo,
  centres_departements_pdl
)

index_dep_pdl

 [1] 4 4 4 4 4 4 4 4 4 4 5 4 5 5 5 3 2 5 5 4 5 4 1 2 5 4 4 4 4 1 5 5 5 5 5 3 4 4
[39] 4 4 5 4 4 2 1 4 5 5 5 2 3 4 4 3 4 4 1 4 4 4 4 3 4 4 5 5 5 4 4 4 4 4 4 4 4 4
[77] 4 4 4 2 4 5 5 2 2 5 2 2 4 4 4 4 4 4 4 4

st_nearest_feature() renvoie un vecteur d’index en résultat.

Pour visualiser cet index, vous pouvez utiliser ensuite la fonction st_nearest_point() qui va permettre de faire un lien entre les départements et le département ligérien le plus proche.

st_nearest_point() permet en effet de renvoyer pour deux géométries la ligne rejoignant les 2 points les plus proches.

liens <- st_nearest_points(departements_geo,
  centres_departements_pdl[index_dep_pdl, ],
  pairwise = TRUE
)

ggplot() +
  geom_sf(data = departements_geo) +
  geom_sf(data = liens)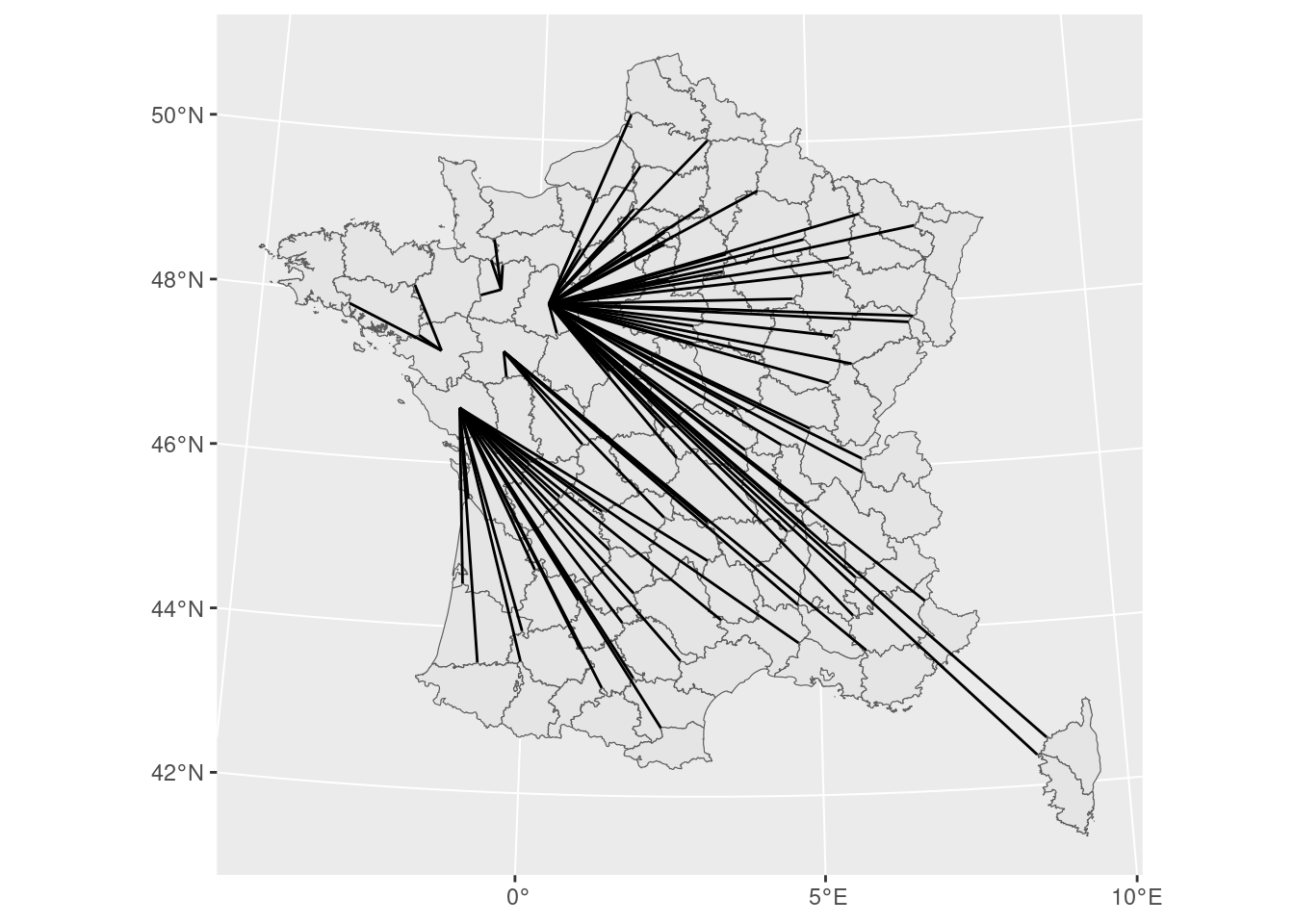

On peut utiliser aussi st_nearest_feature() comme un mode de jointure des données.

departements_join <- st_join(departements_geo,
  centres_departements_pdl,
  join = st_nearest_feature
)

ggplot() +
  geom_sf(data = departements_join, aes(fill = NOM_DEP.y)) +
  labs(
    title = "Département ligérien le plus proche de chaque département français",
    fill = NULL
  )

6.5 Carroyage

6.5.1 Créer une grille régulière

La fonction st_make_grid() permet de créer une grille régulière à partir d’un objet géo. Elle produit un objet rectangulaire de type sfc, il faut ensuite utiliser la fonction st_sf() pour transformer cet objet sfc en objet sf.

Lors de cette transformation nous rajoutons ici une colonne d’identifiants uniques.

grille <- st_make_grid(epci_d44, cellsize = 10000) %>% 
  st_as_sf() %>% 
  rowid_to_column("id")

mapview(grille) + mapview(epci_d44, col.regions = "white", alpha.regions = 0.5)

On constate que plusieurs carreaux sont inutiles. On peut réduire leur nombre avec st_intersects() comme vu précédemment.

grille_ajustee <- grille[epci_d44, , op = st_intersects]
mapview(grille_ajustee) + mapview(epci_d44, col.regions = "white", alpha.regions = 0.5)

6.5.2 Compter des points dans un polygone

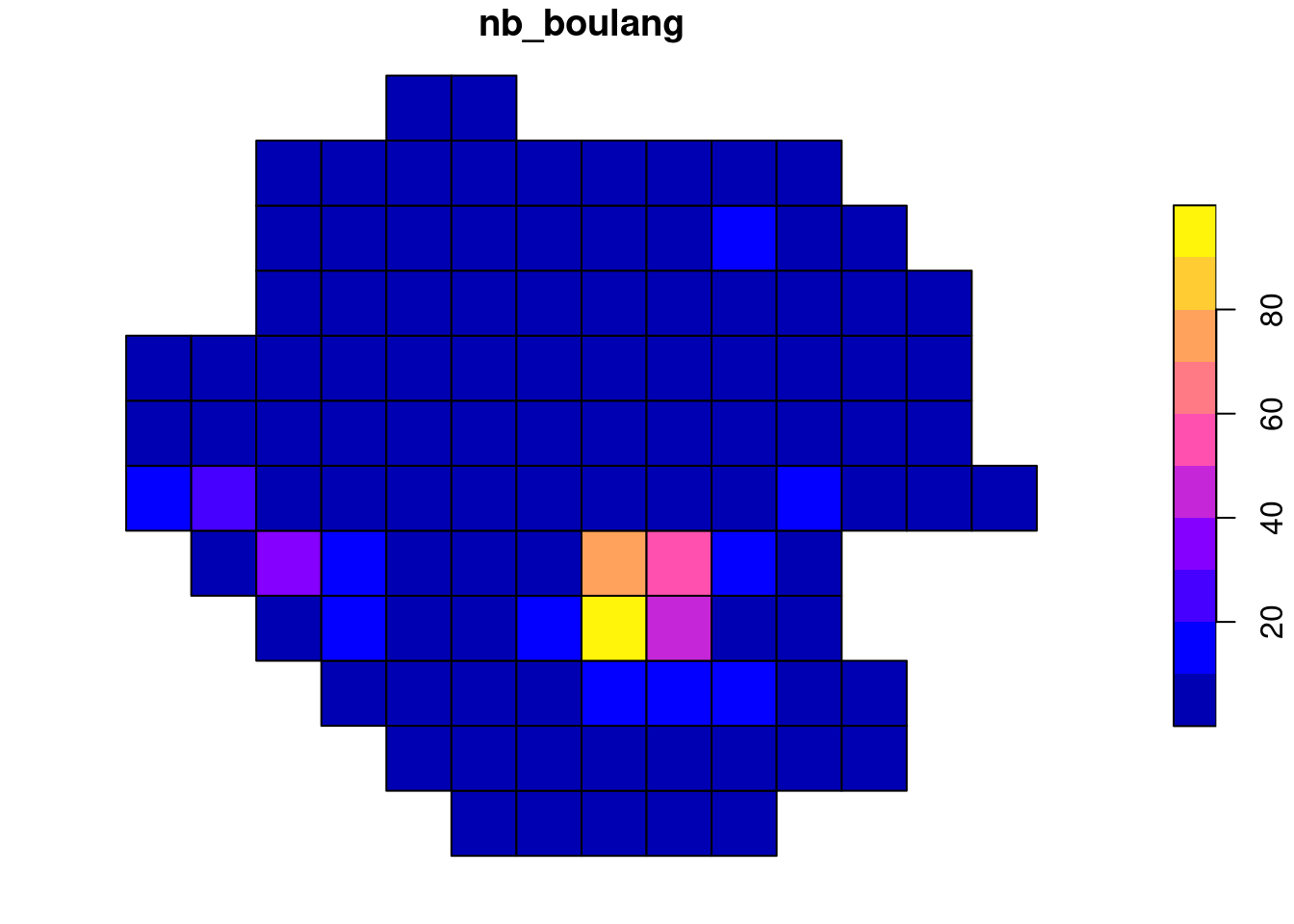
On cherche ici à compter par carreau, le nombre d’entreprises de type “Boulangerie et boulangerie-pâtisserie” (code APE 1071C) du fichier sirene 44 .

boul_44 <- filter(sirene44, APET700 == "1071C") %>% select(SIREN, NOMEN_LONG)
mapview(grille_ajustee) + mapview(epci_d44, col.regions = "white", alpha.regions = 0.5) + mapview(boul_44, col.regions = "grey")

La grille ajustée comprend 113 carreaux. Le 44 comprend 717 boulangeries.

intersection <- st_intersects(grille_ajustee, boul_44, sparse = TRUE)

dim(intersection)

[1] 113 717

L’objet intersection est une liste de la longueur de l’objet grille_ajustee et chaque élément de la liste contient le ou les index des éléments de l’objet boul_44 qu’il intersecte. Exemple avec le 46e carreau :

intersection[[46]]

[1]  92 359 383 652 653 655

Le 46e carreau comprend les boulangeries des lignes 92, 359, 383, 652, 653, 655 de la table boul_44.

Pour compter le nombre de boulangeries par carreau, on peut parcourir la liste et reporter la longueur de chacun de ces éléments.

grille_boul <- mutate(grille_ajustee, nb_boulang = map_dbl(intersection, length))
select(grille_boul, nb_boulang) %>% 
  plot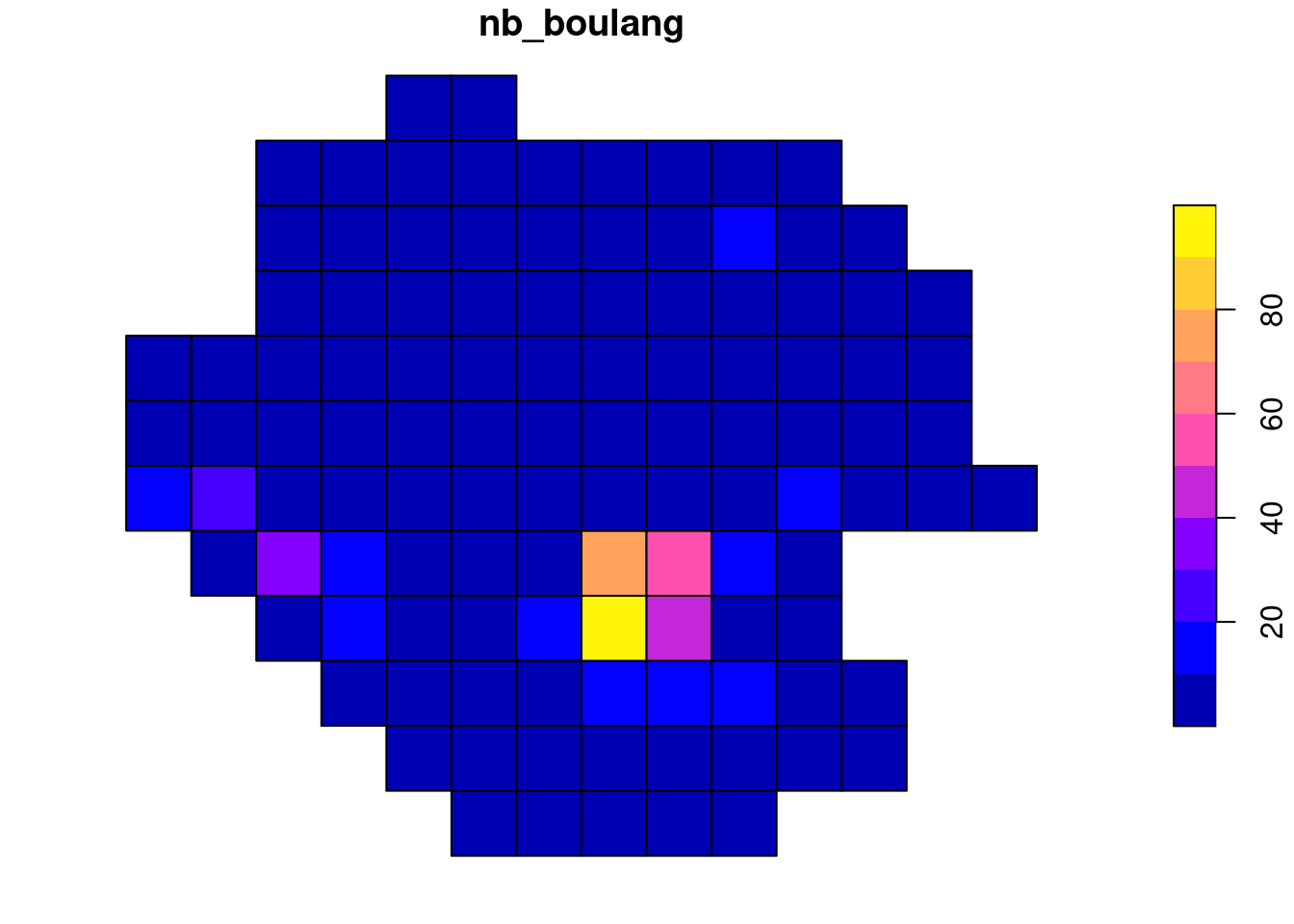

Une autre solution est de passer par les jointures spatiales :

nb_boul_par_carreau <- st_join(x = grille_ajustee, y = boul_44) %>% 
  group_by(id) %>% 
  summarise(nb_boulang = length(SIREN))

select(nb_boul_par_carreau, nb_boulang) %>% plot