Chapitre 7 Les opérations géométriques
Nous allons voir dans ce chapitre comment opérer des opérations géométriques sur nos vecteurs.
Dans ce chapitre, nous allons utiliser les packages suivants.
# CRAN
library(sf)
library(tidyverse)
library(mapview)
library(rmapshaper)
library(cowplot)On distingue deux types d’opérations : les opérations unaires et binaires.
7.1 Opérations unaires
7.1.1 Simplification
La simplification revient comme son nom l’indique à simplifier une couche vectorielle. Le cas d’usage d’un tel procédé peut être un changement d’échelle et plus généralement le besoin de réduire la taille de stockage de notre objet (par exemple pour une publication ou une carte interactive).
Le package sf contient une fonction st_simplify qui implémente l’algorithme de Douglas-Peucker9 de GEOS.
La fonction utilise le paramètre dTolerance pour controler le niveau de simplification.
load("extdata/admin_express.RData")departement_56 <- departements_geo %>%
filter(INSEE_DEP == "56")
departement_56_simplifie <- departement_56 %>%
st_simplify(dTolerance = 900)
departement_56_super_simplifie <- departement_56 %>%
st_simplify(dTolerance = 2000)p1 <- ggplot() +
geom_sf(data = departement_56) +
theme_void() +
theme(panel.grid = element_blank(), panel.border = element_blank())
p2 <- ggplot() +
geom_sf(data = departement_56_simplifie) +
theme_void()
p3 <- ggplot() +
geom_sf(data = departement_56_super_simplifie) +
theme_void()
plot_grid(p1, p2, p3, nrow = 1, labels = c('departement 56', 'simplifié', 'super simplifié'))
On peut mesurer le gain réalisé par chaque opération.
Une simplification avec un
dTolerancede 900 permet d’économiser 91.2 % du stockage.Une simplification avec un
dTolerancede 2000 permet d’économiser 92.2 % du stockage.
object.size(departement_56)451008 bytesobject.size(departement_56_simplifie)39496 bytesobject.size(departement_56_super_simplifie)34976 bytesLe problème de l’algorithme Douglas-Peucker est qu’il simplifie les géométries objet par objet.
Cela conduit à perdre la topologie, et à des trous ou des chevauchements.
L’option preserveTopology = TRUE de st_simplify() doit permettre en théorie d’éviter ce problème, mais ne marche pas au delà d’un certain seuil.
Par exemple, prenons 2 départements autour du Morbihan.
departements_35_44_56 <- departements_geo %>%
filter(INSEE_DEP %in% c("35", "44", "56"))
departements_35_44_56_super_simplifie <- departements_35_44_56 %>%
st_simplify(dTolerance = 3000)p1 <- ggplot() +
geom_sf(data = departements_35_44_56) +
theme_void() +
theme(panel.grid = element_blank(), panel.border = element_blank())
p3 <- ggplot() +
geom_sf(data = departements_35_44_56_super_simplifie) +
theme_void()
plot_grid(p1, p3, nrow = 1)
On constate clairement des trous à la frontière des 3 départements.
Un autre algorithme peut être utilisé qui n’a pas les mêmes limitations, l’algorithme de Visvalingam10.
Le package rmapshaper contient une fonction ms_simplify() qui implémente cet algorithme.
Ce package est une interface vers Mapshaper11, un site en ligne d’édition de données cartographiques.
departements_35_44_56 <- departements_35_44_56 %>%
mutate(AREA = as.numeric(AREA))
departements_35_44_56_ms_simplifie <- ms_simplify(departements_35_44_56, method = "vis", keep = 0.01)p1 <- ggplot() +
geom_sf(data = departements_35_44_56) +
theme_void() +
theme(panel.grid = element_blank(), panel.border = element_blank())
p3 <- ggplot() +
geom_sf(data = departements_35_44_56_ms_simplifie) +
theme_void()
plot_grid(p1, p3, nrow = 1)
7.1.2 Centroïde
Le centroïde permet d’identifier le centre d’un objet géométrique.
Il y a plusieurs façons de définir un centroïde.
La plus usuelle est le centroïde géographique, qui peut être défini comme le point d’équilibre d’un objet (celui en dessous duquel votre doigt peut faire tenir en équilibre cet objet).
La fonction permettant de définir un centroïde dans sf est st_centroid().
centres_departements <- st_centroid(departements_geo)ggplot() +
geom_sf(data = departements_geo) +
geom_sf(data = centres_departements, color = "dark green", size = .5) +
theme_void() +
theme(panel.grid = element_blank(), panel.border = element_blank()) +
labs(title = "les départements et leur centroïdes")
Parfois, le centroïde peut se placer en dehors de l’objet lui même. Par exemple pensez à un atoll.
Dans ce cas, on peut utiliser st_point_on_surface() qui garantit que le point est sur la surface de l’objet de départ.
Egalement, en cas d’objets multipolygonaux, comme par exemple un chapelet d’îlets, la fonction st_centroid() accepte un argument booléen of_largest_polygon à utiliser pour forcer le positionnement du point sur le plus gros polygone.
centr_dep <- st_centroid(departements_geo, of_largest_polygon = TRUE)7.1.3 Buffer
Comme déjà vu, à partir d’une couche de départ de type ponctuel, linéaire ou polygonal, le buffer va créer une nouvelle couche vectorielle. La géométrie de cette couche représente des objets surfaciques dont les frontières sont positionnées à une distance euclidienne, définie par l’utilisateur, des limites des objets vectoriels de la couche de départ.
departement_44 <- departements_geo %>%
filter(INSEE_DEP == "44")
departement_44_buffer <- departement_44 %>%
st_buffer(dist = 5000)
mapview(list(departement_44_buffer, departement_44),
layer.name = list("Loire-Atlantique avec un buffer de 5 km", "Loire-Atlantique"),
zcol = list("NOM_DEP", "NOM_DEP"), col.regions = list("#440154FF", "#FDE725FF"), legend = FALSE)7.2 Opérations binaires
7.2.1 Transformation affine
Les tranformations affines regroupent les transformations qui préservent les lignes et le parallélisme. A l’inverse les angles et les tailles ne le sont pas forcément.
Les transformations affines intègrent notamment les translations, les rotations et les changements d’échelle.
Le package sf implémente ces transformations pour les objets de classe sfg et sfc.
7.2.1.1 Translation
departement_44_sfc <- st_geometry(departement_44)
departement_44_sfc_trans <- departement_44_sfc + c(10000, 10000)
departement_44_trans <- st_set_geometry(departement_44, departement_44_sfc_trans)
st_crs(departement_44_trans) <- st_crs(departement_44)
mapview(list(departement_44_trans, departement_44),
layer.name = list("Loire-Atlantique avec déplacement affine de 10 km vers le nord et 10 km vers le sud", "Loire-Atlantique"),
zcol = list("NOM_DEP", "NOM_DEP"), col.regions = list("#440154FF", "#FDE725FF"), legend = FALSE)7.2.1.2 Changement d’échelle
Dans l’exemple suivant on va réduire par deux la surface de chacun des EPCI du département. Pour cela on va recentrer les EPCI pour que les coodonnées des centroides soient à l’origine, avant de diviser par deux les cordonnées des contours et réappliquer la translation au centroid.
epci_d44 <- st_filter(x = epci_geo, y = departement_44 %>% st_buffer(-3000), .predicate = st_intersects)
epci_d44_sfc <- st_geometry(epci_d44)
epci_d44_centroid_sfc <- st_centroid(epci_d44_sfc)
epci_d44_centroid_sfc_scale <- (epci_d44_sfc - epci_d44_centroid_sfc) * 0.5 + epci_d44_centroid_sfc
epci_d44_centroid_scale <- st_set_geometry(epci_d44, epci_d44_centroid_sfc_scale)
st_crs(epci_d44_centroid_scale) <- st_crs(epci_d44)
mapview(list(epci_d44, epci_d44_centroid_scale),
layer.name = list("Epci de Loire-Atlantique", "Epci de Loire-Atlantique avec surface divisées par deux"),
zcol = list("NOM_EPCI", "NOM_EPCI"), col.regions = list("#440154FF", "#FDE725FF"), legend = FALSE)7.2.2 Découpage
Le découpage spatiale est une forme de filtre sur les géographies.
Le découpage peut seulement s’appliquer à des formes plus complexes que des points : (multi-)lignes, (multi-)polygones.
Nous allons illustrer le découpage à partir des EPCI à cheval sur plusieurs départements.
epci_redon <- epci_d44 %>%
filter(CODE_EPCI == "243500741")
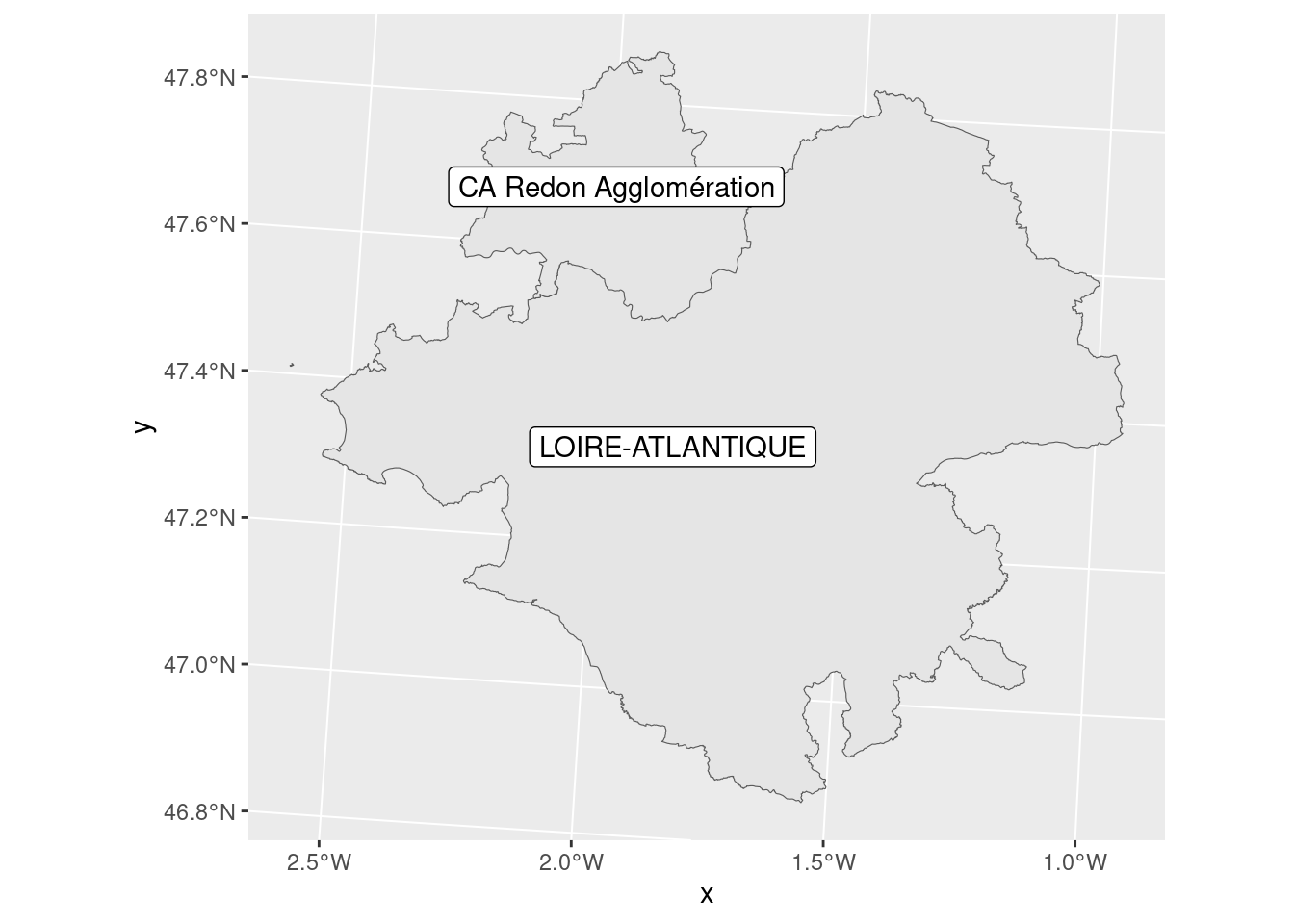
st_intersection() permet de garder la partie commune des deux géométries.
redon_et_departement_44 <- st_intersection(epci_redon, departement_44) %>%
mutate(NOM_EPCI = "Communes du 44\ndans la CA de Redon")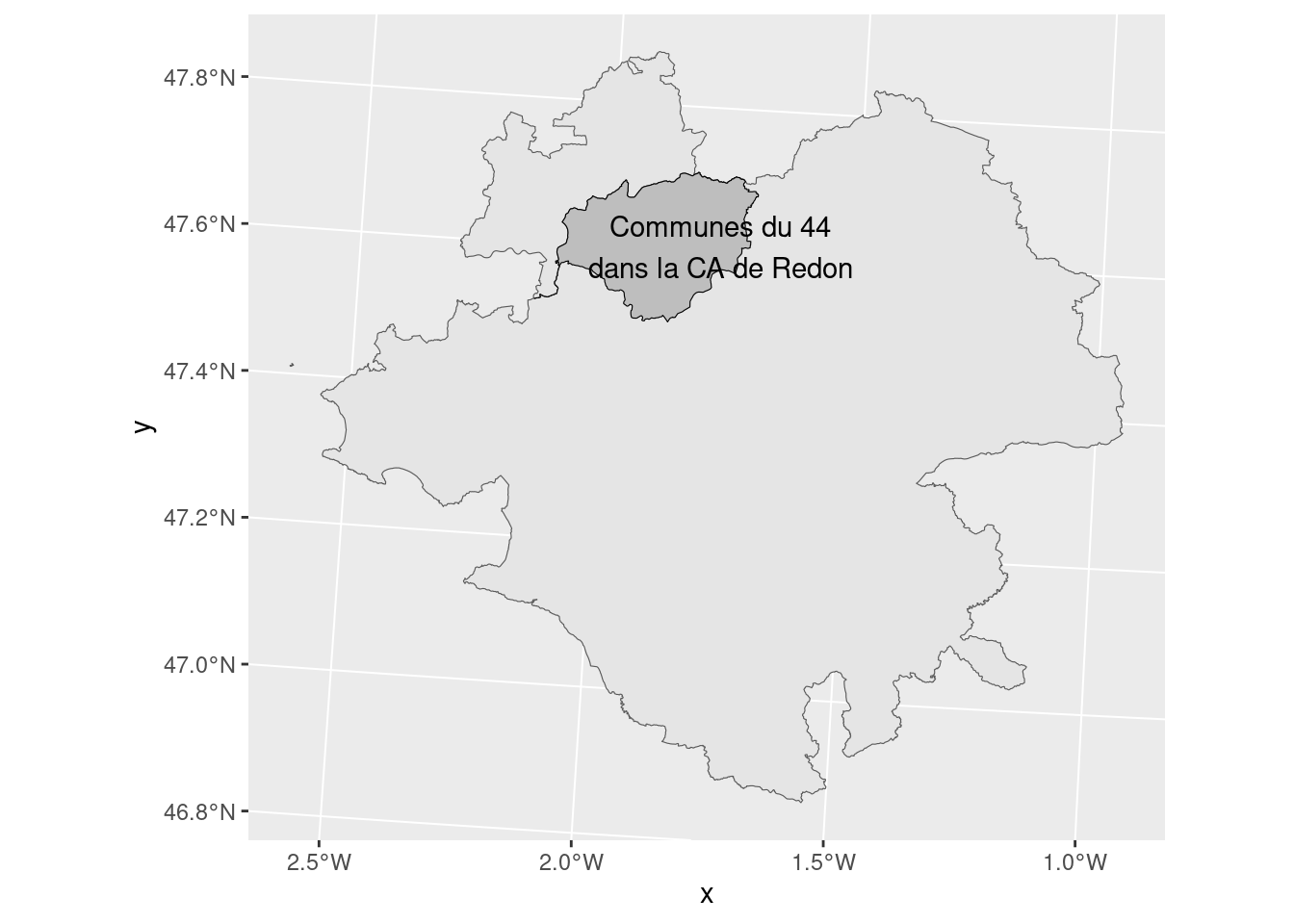
st_difference(x,y) permet de ne garder que la partie de x absente de y
redon_hors_departement_44 <- st_difference(epci_redon, departement_44) %>%
mutate(NOM_EPCI = "Com. de la CA de Redon hors 44")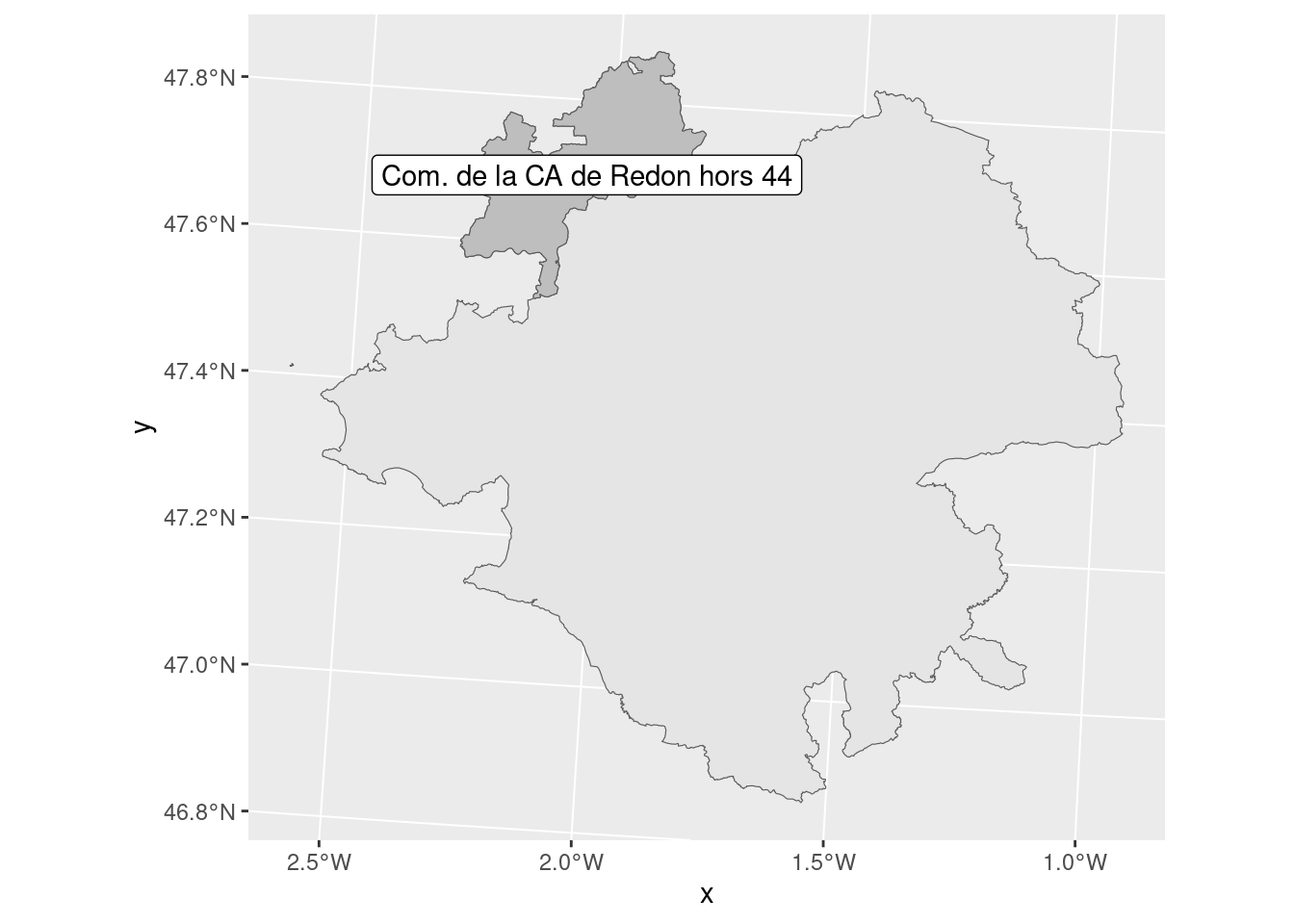
st_sym_difference(x,y) permet de ne garder que les parties de distinctes x et de y.
redon_et_departement_44_sans_partie_communes <- st_sym_difference(epci_redon, departement_44) %>%
mutate(NOM_EPCI = "Communes du 44 et du CA Redon Agglomération hors communes en commun")