Chapitre 2 Les analyses multivariées

2.1 Objectifs

On dispose d’un grand volume de données :

  • \(n\) individus
  • \(p\) variables, avec \(p>2\), potentiellement de natures différentes (qualitatives, quantitatives, binaires…)

\(\Rightarrow\) On ne peut pas examiner tous les croisements des variables 2 à 2.

L’analyse multidimensionelle permet de croiser toutes les variables simultanément et de synthétiser l’information.

Les méthodes présentées ici entrent dans la famille des statistiques exploratoires, très utiles pour défricher certains jeux de données. Par contre, en général elles ne permettent pas directement de tester des hypothèses et encore moins d’inférer des causalités.

2.2 Comment synthétiser ?

  • On souhaite passer d’un espace trop grand, non visualisable (\(p\) dimensions) à un espace plus petit (moins de dimension).
  • Mais on souhaite conserver l’essentiel de la variabilité entre individus \(\Rightarrow\) Concept d’inertie du nuage de points.

Solution : On construit un nouvel espace, dans lequel l’inertie est concentrée sur les premiers axes factoriels. Autrement dit, on construit des nouvelles variables (qui définissent le nouvel espace), combinaisons linéaires des variables initiales, pour lesquelle l’inertie est maximale sur le nombre le plus réduit possible.

2.3 Quelles méthodes ?

Une première partie sera consacrée aux analyses factorielles. Ces dernières permettent de voir rapidement les corrélations ou liens entre variables dans le jeu de données, et de diminuer l’espace d’analyse en construisant des variables synthétiques. Quelques exemples :

  • ACP (analyse en composantes principales) : analyse de \(p\) variables quantitatives
  • AFC (analyse factorielle des correspondances) : analyse de 2 variable qualitatives
  • ACM (analyse des correspondances multiples) : analyse de \(p\) variable qualitatives
  • etc…

Quand on emploie ces méthodes, la procédure à suivre est toujours la même :

  • Implémentation de la méthode choisie \(\rightarrow\) création d’un objet R.
  • Choix du nombre de variables synthétiques retenues.
  • Interprétation des résultats :
    • Comment sont corrélées les variables initiales ?
    • Quel sens puis-je donner à mes variables synthétiques ?
    • Est-ce que des groupes d’individus se dégagent ?

On verra enfin deux méthodes de classification (attention pour vos recherches en anglais : clustering est le terme correspondant ; classification fait référence aux algorithmes de discrimination). Ces méthodes visent à regrouper \(n\) individus en \(k\) classes, à partir de \(p\) variables (continues ou qualitatives). Quelques exemples :

  • CAH (classification ascendante hiérarchique)
  • K-moyennes ou “nuées dynamiques”
  • DBscan
  • X-means

Une ressource inestimable pour les méthodes de clustering (et le machine learning en général) : Page de Scikit-lean.

2.4 Lien entre ces méthodes

  • Toutes visent à diminuer la dimension de l’espace d’analyse et à résumer au mieux l’information.
  • Elles se basent toutes sur le critère d’inertie, autrement dit sur l’hétérogénéité des individus.
  • Pour toutes, il faut choisir le nombre de variables (ou de classes) à retenir.
  • Les analyses factorielles permettent de repérer les variables qui permettent le plus de résumer l’information.
  • La classification permet de regrouper les individus aux caractéristiques proches. C’est la méthode la plus synthétique, donc la plus réductrice.
  • Il est souvent pertinent d’utiliser une analyse factorielle + une méthode de partitionnement en complément pour bien comprendre l’information contenue dans les données.

2.5 Notion de distance

On parle de proximité entre les individus \(\Rightarrow\) comment la mesurer ? Par une distance.

Exemple de la distance euclidienne en 3D : \(D = \sqrt{(x_{b}-x_{a})^2+(y_{b}-y_{a})^2+(z_{b}-z_{a})^2}\)

Il existe de nombreuses autres distances qui répondent à différents usages. En restant dans le domaine des distances géographiques, il existe par exemple la distance orthodromique, utilisée par les marins, qui est la plus courte à la surface du globe terrestre entre deux points (calculable avec les packages geosphere ou fields), ou la distance curviligne le long d’un réseau hydrographique utilisée par les hydrologues (calculable avec le package riverdist).

En génétique des populations, on utilise la distance génétique pour mesurer le degré de dissemblance entre deux génomes.

En écologie des communautés, l’indice de Jaccard permet de comparer la composition en espèces de deux communautés A et B. C’est le pourcentage du nombre total d’espèces présentes dans au moins un des échantillons qui est commun aux deux échantillons :

\(J(A,B) = \frac{|A \cap B|}{|A \cup B|}\)

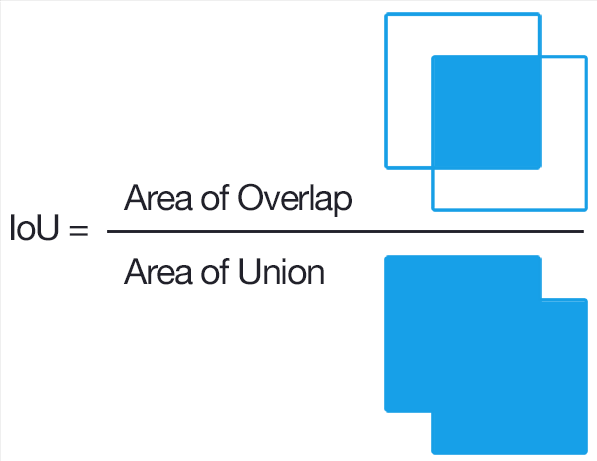
C’est donc un indice de proximité qui varie de 0% (aucune espèce n’est commune aux deux échantillons) à 100% (toutes les espèces sont communes à A et à B).

La distance de Jaccard est \(D_j = 1 - J\).

\(\Rightarrow\) Il existe de nombreuses autres distances correspondant à différents usages et métiers.

En statistiques, on est amené à utiliser des distances “exotiques” en plus de la distance euclidienne et de la distance de Jaccard : Distance du \({\chi}^2\) (en AFC et ACM), Mahalanobis, Bray-Curtis …

2.6 Questions à se poser

Mon objectif est de :

  1. Déterminer une typologie \(\Rightarrow\) classification / partitionnement.
  2. Explorer des liens entre variables et entre individus \(\Rightarrow\) analyses factorielles.

Puis, si l’on est dans le cas n°2, cette petite vidéo (en anglais, mais l’accent de l’auteur aide à la compréhension) donne un rapide aperçu des questions à se poser avant de se lancer dans les analyses. On peut la résumer ainsi :

  1. Que représente mon tableau de données ?
    • Un tableau de contingence \(\Rightarrow\) AFC
    • Un tableau de \(n\) individus x \(p\) variables \(\Rightarrow\) aller au point 4.

  2. Quels sont les éléments (lignes, colonnes) qui seront “actifs”, c’est-à-dire qui participeront à la constitution des axes, donc à la détermination des distances entre les individus ? Les autres éléments, dits “supplémentaires”, pourront être positionnés après coup sur les axes.

  3. Les variables sont-elles quantitatives ou qualitatives ?
    • Quantitatives \(\Rightarrow\) ACP
    • Qualitatives, 2 variables et tableau de contingence \(\Rightarrow\) AFC
    • Qualitatives, autres cas \(\Rightarrow\) ACM

  4. Si l’on est dans le cas de l’ACP, doit-on standardiser les variables ?

  5. Y a-t-il des valeurs manquantes dans le tableau à analyses ? Si oui, comment les gérer ?

2.7 Nature des variables

On distingue les variables qualitatives des variables quantitatives. Cependant, cette distinction n’est pas absolument évidente.

2.7.1 Variables quantitatives

Une variable quantitative permet de mesurer une grandeur (quantité). Elle peut être :

  • discrète (un nombre fini de valeurs possibles). Exemple : un nombre de logements

  • continue (a priori, toutes les valeurs possibles). Exemple : une taille, une surface, un revenu

2.7.2 Variables qualitatives

Une variable qualitative indique des caractéristiques qui ne sont pas des quantités. Les différentes valeurs que peut prendre cette variable sont appelées les catégories ou modalités (levels dans R). Elle peut être :

  • ordonnée (exprimer un ordre). Exemple : “petit - moyen - grand”

  • non ordonnée. Exemple : une couleur, un groupe sanguin…

2.7.3 Entre les deux

Les variables binaires (ou boléennes) peuvent être considérées soit comme quantitatives, soit comme qualitatives.

Les variables ordinales peuvent être codées quantitativement, comme par exemple un indice de satisfaction dans une enquête : - 0 : Pas satisfait du tout - 1 : Plutôt pas satisfait - 2 : Plutôt satisfait - 3 : Très satisfait Dans un tel cas, ce n’est pas très élégant car ça dépebd du codage choisi, mais on peut calculer des indices de satisfaction “moyens” par exemple pour comparer des groupes.

À l’inverse, on peut discrétiser une variable quantitative pour la transformer en variable qualitative, avec la fonction cut et en précisant les bornes du découpage. En discrétisant, on perd une part de l’information (l’information intra-classe), donc c’est à éviter autant que possible en privilégiant les méthodes applicables aux variables quantitatives.

2.8 Le package FactoMineR

Il existe de nombreux packages R pour les analyses multivariées : ade4, vegan, cluster, Hmisc, etc. Il a bien fallu choisir.

Le package FactoMineR est décrit dans cet article du J. Stat. Software de 2008. Il a donc fait ses preuves. Il est très employé : en décembre 2018, l’article est cité plus de 1800 fois depuis 2008 dans Google Scholarhttps://scholar.google.fr/scholar?as_q=factominer&as_epq=&as_oq=&as_eq=&as_occt=any&as_sauthors=husson&as_publication=&as_ylo=&as_yhi=&hl=fr&as_sdt=0%2C5.

Il permet de réaliser toutes les analyses multivariées usuelles et fournit de nombreuses aides graphiques à l’interprétation \(\Rightarrow\) “école française de l’analyse multivariée”.

Deux de ses fonctionnalités sont particulièrement intéressantes :

  • La possibilité de projeter des variables ou des individus supplémentaires.
  • La simplicité d’utilisation avec le package missMDA pour imputer les valeurs manquantes.

La documentation associée est très riche, dont une bonne partie en français. Il y a en particulier :

Il existe un module complémentaire pour améliorer les graphiques de sortie : Factoshiny.

La plupart des méthodes qui ne sont pas comprises dans FactoMineR peuvent être mises en oeuvre avec le package ade4, en particulier pour l’analyse discriminante et les analyses à plusieurs tableaux (co-inertie, ACP sur variables instrumentales, analyse canonique des correspondences, analyse RLQ).