Chapitre 5 Une variable qualitative

Les données qualitatives peuvent faire l’objet de dénombrement, en effectif ou en proportion.

Petit rappel : cours en ligne et liens avec Excel.

Pour décrire une variable qualitative, on calcule :

Le nombre d’occurrence de chacune des modalités dans la base (ex : le nombre de communes de chaque type ZAU) : \(N_i\) où \(i \in \{1 ... k\}\) représente l’ensemble des modalités
La proportion (ou fréquence) de chacune des modalités : \(f_i = \frac{N_i}{N}\)

On peut calculer des effectifs pondérés (exemple : la population des communes de chaque type ZAU). Dans ce cas \(N_i = \sum_c w_i\cdot \mathbb{I}_{c = i}\) et \(N = \sum_c w_i\), où c est l’ensemble des communes.

Pour un premier coup d’oeil à une variable qualitative, on peut utiliser la fonction générique summary().

select (dat, ZAU) %>%
  summary ()

##      ZAU           
##  Length:36689      
##  Class :character  
##  Mode  :character

5.1 Tableaux de synthèse

5.1.1 Comptage

On cherche le nombre d’occurence de chacune des modalités. Cela s’effectue grâce à la fonction table().

pull (dat, ZAU) %>%
  table ()

## .
##       111 - Grand pôle (plus de 10 000 emplois) 
##                                            3285 
##                  112 - Couronne d'un grand pôle 
##                                           12297 
## 120 - Multipolarisée des grandes aires urbaines 
##                                            3962 
##       211 - Moyen pôle (5 000 à 10 000 emplois) 
##                                             456 
##                  212 - Couronne d'un moyen pôle 
##                                             815 
##     221 - Petit pôle (de 1 500 à 5 000 emplois) 
##                                             888 
##                  222 - Couronne d'un petit pôle 
##                                             582 
##              300 - Autre commune multipolarisée 
##                                            7021 
##   400 - Commune isolée hors influence des pôles 
##                                            7383

La fonction DT::datatable() permet une mise en forme moins austère des dataframes.

pull (dat, ZAU) %>%
  table () %>%
  as.data.frame () %>%
  datatable (rownames = FALSE, colnames = c ("ZAU", "Nombre"))

5.1.2 Comptage pondéré

On ne cherche plus à afficher le nombre d’occurence de chaque modalités, mais à connaître le poids d’une variable sur ces modalités. Il s’obtient avec la fonction xtabs(). Par exemple, si on veut connaître la population pour chaque ZAU :

xtabs (formula = P14_POP ~ ZAU, data = dat) %>% 
  as.data.frame () %>% 
  datatable (rownames = FALSE, colnames = c ("ZAU", "Population"))

5.1.3 Fréquences

On souhaite maintenant connaître le pourcentage de communes que représente chaque ZAU. Cela se fait grâce à la fonction table() suivi cette fois de prop.table(). Par exemple :

pull (dat, ZAU) %>%
  table () %>%
  prop.table () %>% 
  round (3) %>% 
  as.data.frame () %>%
  datatable (rownames = FALSE, colnames = c ("ZAU", "Fréquence")) %>%
  formatPercentage ('Freq', 1)

5.1.4 Fréquences pondérées

On souhaite finalement connaître le pourcentage de population que représente chaque ZAU. En respecant la même logique que précédemment : cela se fait grâce à la fonction xtabs() suivi de prop.table(). Par exemple :

xtabs (formula = P14_POP ~ ZAU, data = dat) %>% 
  prop.table () %>% 
  round (3) %>% 
  as.data.frame () %>% 
  datatable (rownames = FALSE, colnames = c("ZAU", "% de la Population"))%>%
  formatPercentage('Freq', 1)

5.2 Graphiques

5.2.1 Diagramme en barres (ou en bâtons)

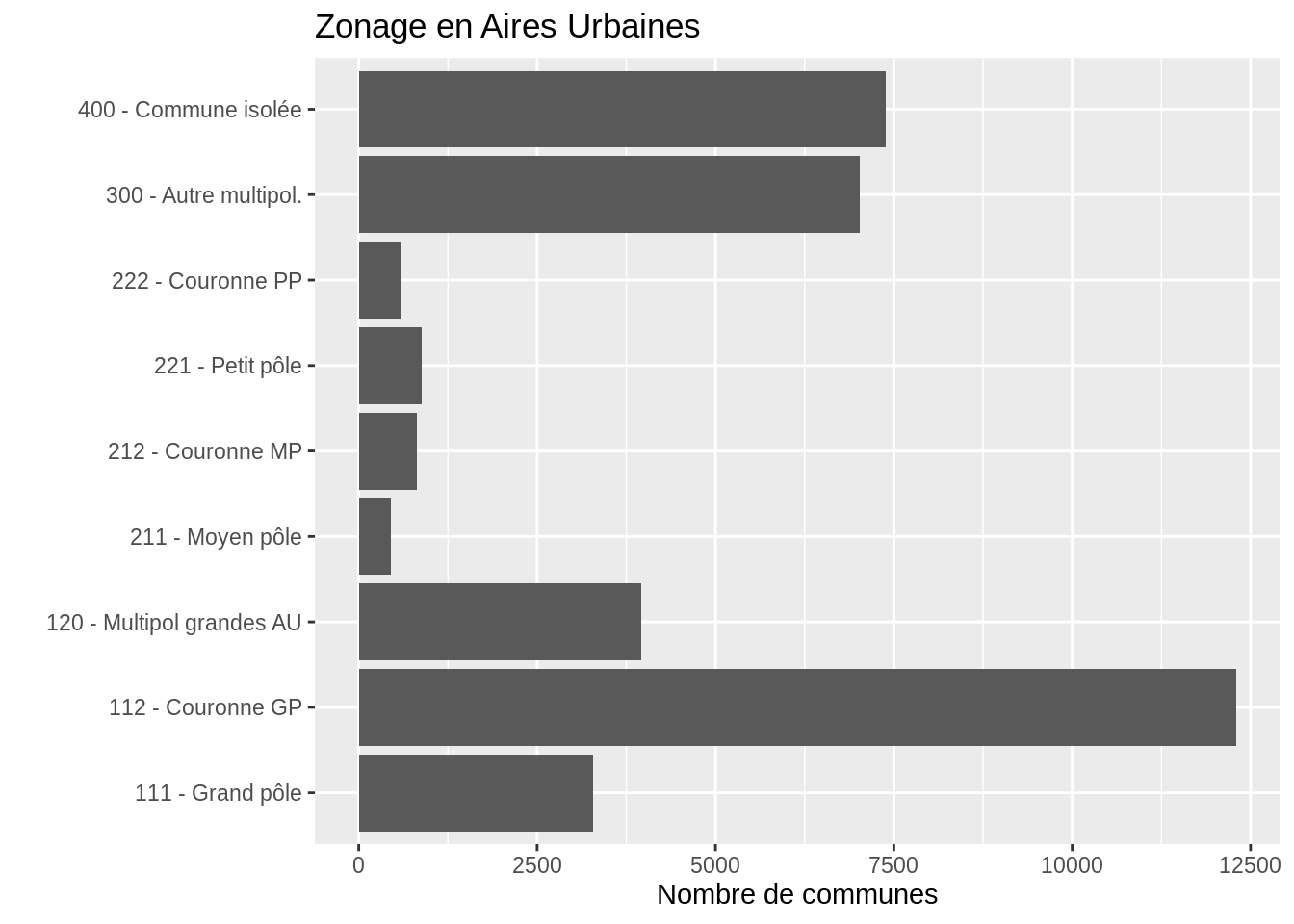
On souhaite connaître le nombre de communes dans chaque ZAU. Grâce à notre base communale, on cherche donc le nombre de lignes pour chaque ZAU.

ggplot (dat, aes (x = ZAU2, fill = ZAU2)) +
  geom_bar () +
  ggtitle ("Zonage en Aires Urbaines") +
  xlab (label = "Classe typolgique ZAU") + 
  ylab (label = "Nombre de communes") +
  theme (axis.text.x = element_blank ()) +
  theme(legend.title = element_blank())

## Warning in min(x): no non-missing arguments to min; returning Inf

## Warning in max(x): no non-missing arguments to max; returning -Inf

## Warning: Removed 36689 rows containing non-finite outside the scale range
## (`stat_count()`).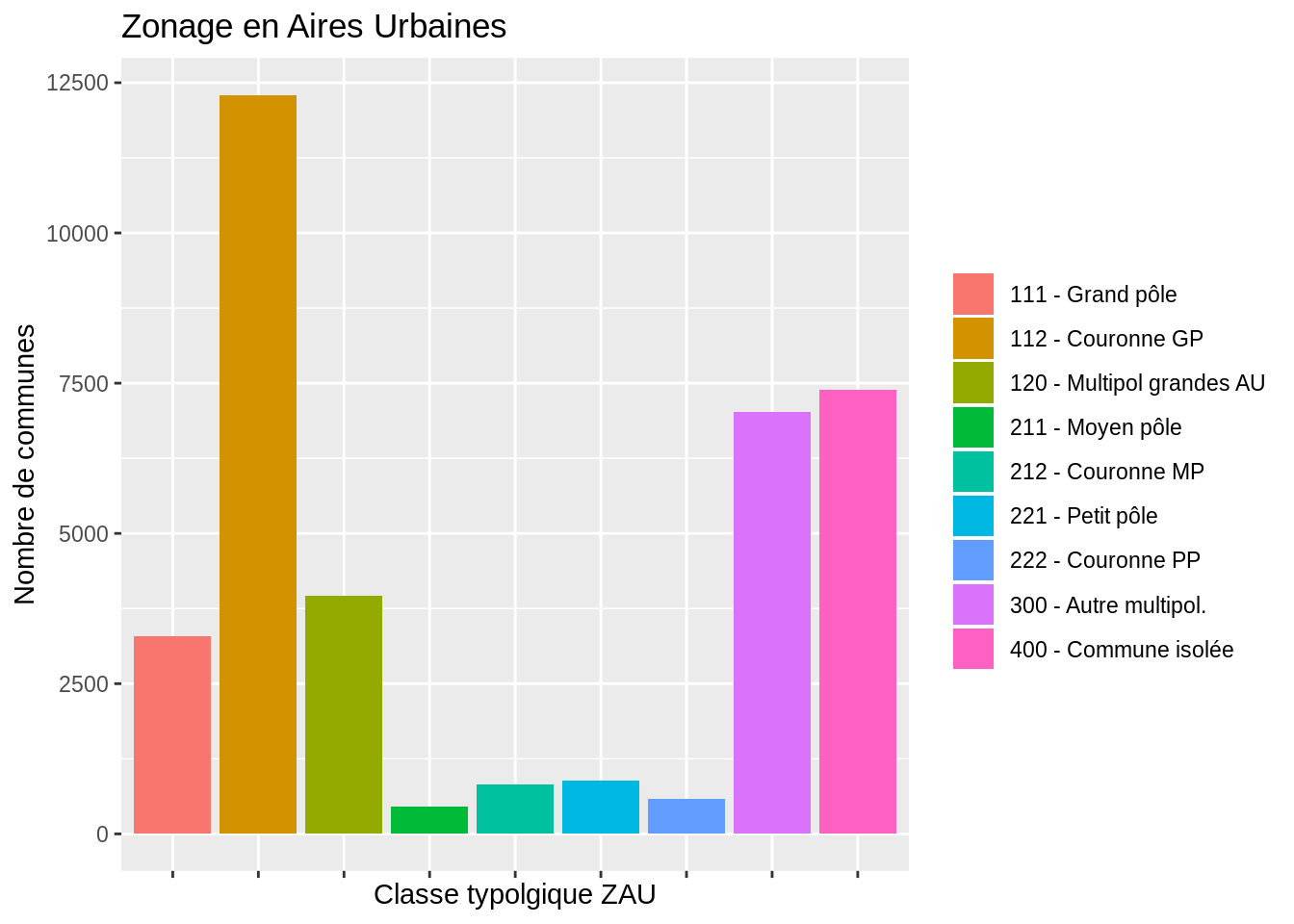

Ceci n’est pas un histogramme ! C’est un diagramme en barres. La lisibilité est compliqué en raison de l’ordre des facteurs. Grâce aux fonctions vues précédemment, on peut modifier cet ordre :

ggplot (dat, aes (x = fct_infreq (ZAU2), fill = fct_infreq (ZAU2))) +
  geom_bar () +
  ggtitle ("Zonage en Aires Urbaines") +
  xlab (label = "Classe typolgique ZAU") + 
  ylab (label = "Nombre de communes") +
  theme (axis.text.x = element_blank ()) +
  theme(legend.title = element_blank())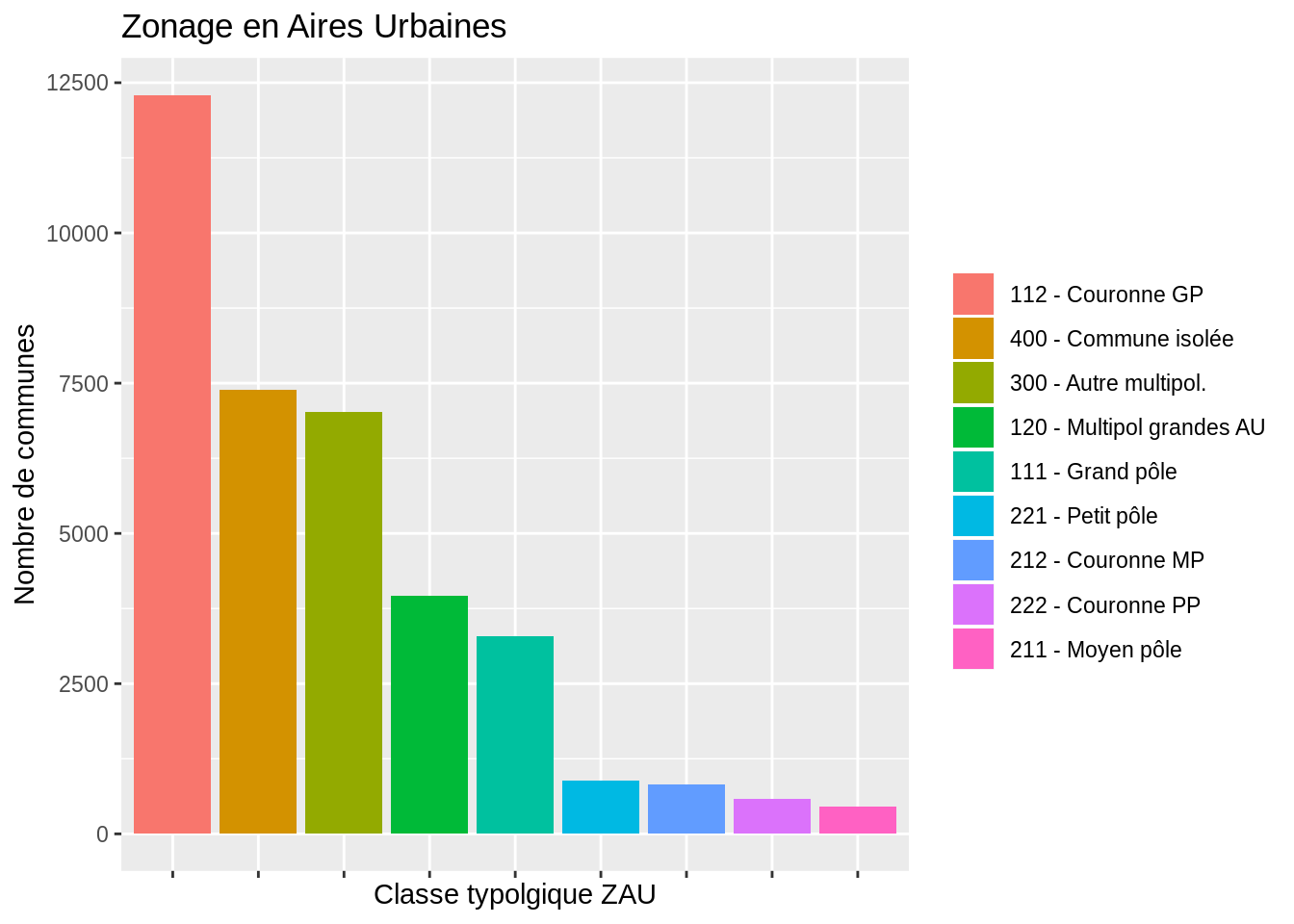

D’autres présentations sont possibles. Par exemple, avec les intitulés des modalités sur l’axe (obtenu grâce à coord_flip(), il n’y donc plus besoin de différencier par les couleurs, ni de la légende. La disposition en barres horizontales permet d’afficher ces intitulés longs.

ggplot (dat, aes (x = ZAU2)) +
  geom_bar () +
  ggtitle ("Zonage en Aires Urbaines") +
  ylab (label = "Nombre de communes") +
  xlab ("") +
  theme (legend.position = "none") +
  coord_flip ()

## Warning in min(x): no non-missing arguments to min; returning Inf

## Warning in max(x): no non-missing arguments to max; returning -Inf

## Warning: Removed 36689 rows containing non-finite outside the scale range
## (`stat_count()`).

5.2.2 Diagramme en secteurs

Cette forme est à éviter autant que possible car sa lecture est moins facile que celle des diagrammes en barres. Elle s’obtient grâce à coord_polar().

ggplot (dat, aes (x = 1, fill = ZAU2)) +
  geom_bar () +
  coord_polar (theta = "y")